
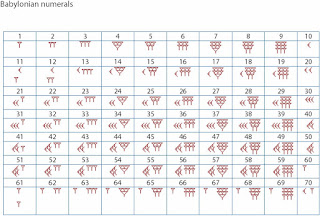
Here are the 59 symbols built from these two symbols This is because the 59 numbers, which go into one of the places of the system, were built from a 'unit' symbol and a 'ten' symbol. Now although the Babylonian system was a positional base 60 system, it had some vestiges of a base 10 system within it. However, rather than have to learn 10 symbols as we do to use our decimal numbers, the Babylonians only had to learn two symbols to produce their base 60 positional system. Now of course this comment is based on knowledge of our own decimal system which is a positional system with nine special symbols and a zero symbol to denote an empty place.

Often when told that the Babylonian number system was base 60 people's first reaction is: what a lot of special number symbols they must have had to learn. Some would argue that it was their biggest achievement in mathematics. Yet neither the Sumerian nor the Akkadian system was a positional system and this advance by the Babylonians was undoubtedly their greatest achievement in terms of developing the number system. From the number systems of these earlier peoples came the base of 60, that is the sexagesimal system. Certainly in terms of their number system the Babylonians inherited ideas from the Sumerians and from the Akkadians. We give a little historical background to these events in our article Babylonian mathematics. The Pythagorean rule was also known to the Babylonians.The Babylonian civilisation in Mesopotamia replaced the Sumerian civilisation and the Akkadian civilisation.

The volume of a cylinder was taken as the product of the base and the height, however, the volume of the frustum of a cone or a square pyramid was incorrectly taken as the product of the height and half the sum of the bases. They were aware that this was an approximation, and one Old Babylonian mathematical tablet excavated near Susa in 1936 (dated to between the 19th and 17th centuries BC) gives a better approximation of π as 25/8 = 3.125, about 0.5 percent below the exact value. They measured the circumference of a circle as three times the diameter and the area as one-twelfth the square of the circumference, which would be correct if π is estimated as 3. 28 (3), p. 202).īabylonians knew the common rules for measuring volumes and areas. Robson, "Neither Sherlock Holmes nor Babylon: a reassessment of Plimpton 322", Historia Math. Most satisfactorily by reciprocal pairs, as first suggested half a century ago, and the second Same answer as the question "what problems does the tablet set?" The first can be answered the question "how was the tablet calculated?" does not have to have the Care must be exercised to see the tablet in terms of methods familiar or accessible to scribes at the time. Much has been written on the subject, including some speculation (perhaps anachronistic) as to whether the tablet could have served as an early trigonometrical table. The triples are too many and too large to have been obtained by brute force. The Babylonian tablet YBC 7289 gives an approximation to 2. The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics that include fractions, algebra, quadratic and cubic equations and the Pythagorean theorem. Written in Cuneiform script, tablets were inscribed while the clay was moist, and baked hard in an oven or by the heat of the sun. In contrast to the scarcity of sources in Egyptian mathematics, knowledge of Babylonian mathematics is derived from some 400 clay tablets unearthed since the 1850s. Babylonian mathematics remained constant, in character and content, for over a millennium. With respect to content, there is scarcely any difference between the two groups of texts. With respect to time they fall in two distinct groups: one from the Old Babylonian period (1830–1531 BC), the other mainly Seleucid from the last three or four centuries BC. Babylonian mathematical texts are plentiful and well edited. The tablet also gives an example where one side of the square is 30, and the resulting diagonal is 42 25 35 or 42.4263888.īabylonian mathematics (also known as Assyro-Babylonian mathematics ) are the mathematics developed or practiced by the people of Mesopotamia, from the days of the early Sumerians to the centuries following the fall of Babylon in 539 BC. The diagonal displays an approximation of the square root of 2 in four sexagesimal figures, 1 24 51 10, which is good to about six decimal digits.ġ + 24/60 + 51/60 2 + 10/60 3 = 1.41421296. Babylonian clay tablet YBC 7289 with annotations.


 0 kommentar(er)
0 kommentar(er)
